有句話我們大家都很熟悉:聽(tīng)過(guò)很多大道理,卻仍然過(guò)不好這一生。于是乎,有人覺(jué)得原因是出在這些“大道理”上,是這些“大道理”的道理還不夠深刻,所以沒(méi)有改變我們的命運(yùn),沒(méi)有讓我們過(guò)好這一生。
但是,越是活的成功,越是活的通透的人,在他們眼里,他們活的就是那些簡(jiǎn)單的“大道理”。那同樣是“大道理”,為什么有的人能夠活的很成功,而另一些人活的渾渾噩噩呢?答案就在于兩個(gè)字:
踐行
一切道理靠踐行,一切的成功,也都靠踐行。只是嘴上說(shuō)的過(guò)癮,如果沒(méi)有真正的沉下身子去老老實(shí)實(shí)的去執(zhí)行,是萬(wàn)不可能成功的。
有個(gè)笑話是這樣講的:一個(gè)人天天虔誠(chéng)地向上帝祈禱:主啊,讓我彩票中獎(jiǎng)500萬(wàn)吧!每天如此,每天如此。堅(jiān)持了很多天后,有一天,上帝終于降臨在他面前。只見(jiàn)上帝怒氣沖沖地對(duì)他說(shuō):你TM的倒是去買張彩票啊!
所以,在我們考研的歷程中,真的沒(méi)有什么捷徑,真的沒(méi)有什么竅門。有的就是老老實(shí)實(shí)的看書(shū),學(xué)習(xí)和做題,有的就是每天熬夜看書(shū)的痛苦,有的就是每天堅(jiān)持早起背過(guò)的單詞,有的就是受到打擊后仍然認(rèn)為自己能考上的信心。。。。。。
這世間充斥著很多“大道理”,認(rèn)真的去對(duì)待這些樸素的道理,認(rèn)真的在生活工作中,實(shí)踐這些道理,那些最終獲得的成功,在你看來(lái),就是這些道理“生效”了。而“大道理”只是聽(tīng)過(guò),而沒(méi)有嚴(yán)格地,不折不扣地,執(zhí)拗地去執(zhí)行,那持續(xù)的原地踏步,在你看來(lái),就是這些道理“沒(méi)有用”,那你再去尋找什么“更沒(méi)用”的竅門,又怎么能成功呢?
1
絕對(duì)值在我們的考試中還是占據(jù)有一定的分量的,雖然考的不算很多,但是在很多題中都有體現(xiàn)。今天我們來(lái)看一種絕對(duì)值中比較偏難一些的題。我們爭(zhēng)取能在這篇文章中給大家講清楚這類題的背后原理,做題技巧。來(lái),上題:
如果關(guān)于x的不等式|3-x|+|x-2|<a的解集是空集,則a的取值范圍是
A,a<1 B,a≤1 C,a>1 D,a≥1 E,a≠1
這道題正常的做法,就是先將y=|3-x|+|x-2|的圖像畫(huà)出來(lái),然后根據(jù)圖像和y=a相交的情況,來(lái)最終判斷a的范圍。
我們先來(lái)用正常方法做一遍,然后總結(jié)一個(gè)規(guī)律。首先我們將y=|3-x|+|x-2|寫成分段函數(shù):
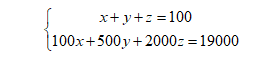
接著我們畫(huà)出該函數(shù)在坐標(biāo)軸中的簡(jiǎn)圖:
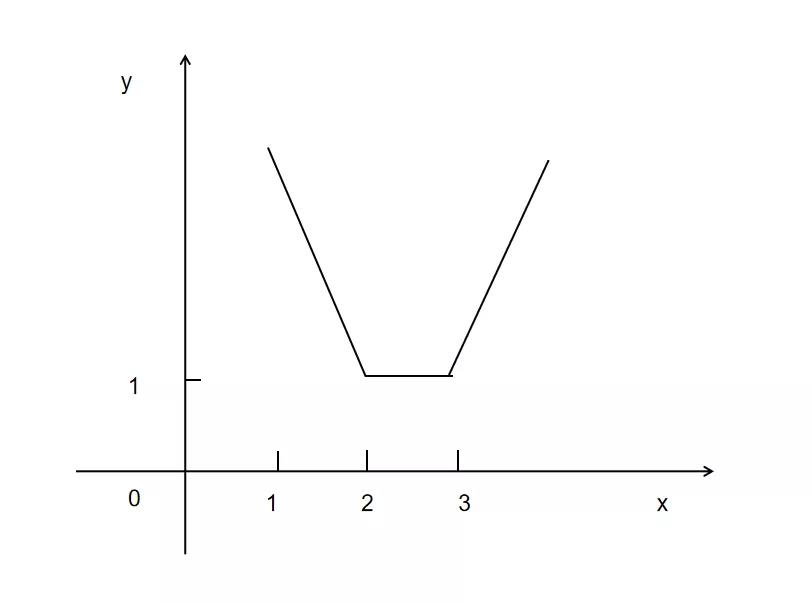
你看看,形狀像不像灰太狼的平底鍋呢?我們把這個(gè)圖形稱為平底鍋模型。
然后題中說(shuō),函數(shù)的值小于a的解集是空集,意思是啥?就是不能小于a唄!不能小于a,啥意思呢?就是大于等于a永遠(yuǎn)成立唄。那啥叫做永遠(yuǎn)大于等于a呢,怎么才能永遠(yuǎn)才能大于等于a呢?只有最小值都大于等于a,才能保證我永遠(yuǎn)大于等于a啊!
舉個(gè)例子:李老師的財(cái)富<馬云的財(cái)富是假的(可以理解成是空集),那就是李老師我的財(cái)富要≥馬云的財(cái)富永遠(yuǎn)成立唄,那我怎么保證我的財(cái)富永遠(yuǎn)大于等于馬云財(cái)富呢,就是我財(cái)富最低的值,都大于等于馬云的財(cái)富,才能說(shuō)我永遠(yuǎn)大于等于馬云的財(cái)富啊!!!(哎哎哎,放下你們手中49米長(zhǎng)的大刀)。
那這道題的關(guān)鍵就在于求解出函數(shù)y=|3-x|+|x-2|的最小值,根據(jù)圖形,我們知道,最小值是1,那就是1大于等于a,即a≤1。這就是答案了。
那能不能再簡(jiǎn)單一些,我們能不能不畫(huà)圖,就找出這類函數(shù)的最小值呢?
當(dāng)然可以啦,類似于y=|3-x|+|x-2|的函數(shù),兩個(gè)絕對(duì)值中間是+號(hào)的,只有最小值,沒(méi)有最大值。最小值是兩個(gè)零點(diǎn)的差的絕對(duì)值。什么是零點(diǎn)呢,就是我們令絕對(duì)值內(nèi)部等于0,得出來(lái)的x的值。比如這個(gè)函數(shù)y=|3-x|+|x-2|的兩個(gè)零點(diǎn)是3和2,那3和2的差是±1,其中的正1就是函數(shù)的最小值(為啥不是-1,因?yàn)閮蓚€(gè)絕對(duì)值相加,不可能是負(fù)數(shù)啊!)
所以類似于y=|x-a|+|x-b|的最小值就是兩個(gè)零點(diǎn)的差,要正的那個(gè),即|a-b|!
2
我們?cè)賮?lái)兩道同類型的題,練練手:
不等式|x-2|+|4-x|<s無(wú)解.
(1)s≤2. (2)s>2.
首先我們判斷函數(shù)y=|x-2|+|4-x|的最小值,兩個(gè)零點(diǎn)是2和4,最小值是4-2=2,圖形是平底鍋模型。|x-2|+|4-x|<s無(wú)解,也就是空集的意思,就是|x-2|+|4-x|不能小于s唄,那就是|x-2|+|4-x|≥s恒成立嘍,那就是2≥s嘍。條件(1)充分,選A。
方程|x+2|+|x-8|=a有無(wú)數(shù)正根.
(1)-4<a<4. (2)a=4.
首先我們判斷函數(shù)y=|x+2|+|x-8|的最小值,兩個(gè)零點(diǎn)是-2和8,最小值是8-(-2)=10,圖形是平底鍋模型。方程|x+2|+|x-8|=a有無(wú)數(shù)正根,說(shuō)明函數(shù)y=|x+2|+|x-8|和函數(shù)y=a有無(wú)數(shù)個(gè)交點(diǎn)啊,那就是函數(shù)y=a的圖像和函數(shù)y=|x+2|+|x-8|的圖像有某條線重合啊!那就只能是和平底鍋的底重合了(y=a平行于x軸,只能和底重合)。重合就是值相等。所以a就是函數(shù)y=|x+2|+|x-8|的最小值,即a=10。這道題選E嘍。
3
那有同學(xué)會(huì)問(wèn)了,老師,上面的都是兩個(gè)絕對(duì)值相加的形式,有沒(méi)有兩個(gè)絕對(duì)值相減的形式呢?當(dāng)然有了,看題:
若不等式|x+3|-|x-6|>a有解,則a的取值范圍是
A,a>-9 B,a≤-9 C,a≤9 D,a<9 E,a>9
這類題的圖形畫(huà)出來(lái)是個(gè)Z字型或者反Z字型(這里要求你自己在圖上畫(huà)一下,驗(yàn)證一下)。不過(guò)具體是Z字型還是反Z字型都無(wú)關(guān)緊要,我們關(guān)心的是最大值和最小值。
那像這類兩個(gè)絕對(duì)值相減的類型,它是有最大值和最小值的。如何確定兩個(gè)最值的大小呢?首先,找零點(diǎn),-3和6。其次,作差,兩個(gè)零點(diǎn)的差,-9和9。好了,-9就是最小值。9就是最大值。So easy!
|x+3|-|x-6|>a有解,意思就是不管a咋樣蹦跶,我都能大于你,意思就是我只需要保證我的最大值能大于你就ok了。最大值是9,那就是9>a,即a<9了。選D。
好了,上面是我們用比較簡(jiǎn)單的形式講解了這類題的做法,我們下面給出通用的模型總結(jié),大家要記好呀!
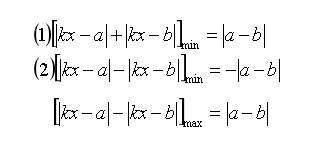
好了,我們這期的內(nèi)容就講到這里啦。感謝大家觀看,歡迎大家點(diǎn)贊收藏點(diǎn)在看。威廉詹姆斯說(shuō)過(guò):人類本質(zhì)中最殷切的需求,是渴望得到他人的肯定。您的支持,是我持續(xù)輸出優(yōu)質(zhì)內(nèi)容的動(dòng)力!我們下期再見(jiàn)!




